번외) 레드 블랙 트리 정리

레드-블랙 트리

이진 트리의 약점을 극복하기 위해 새로운 규칙을 추가하여 나온 이진 트리이다. 자바의 TreeSet과 TreeMap은 레드-블랙 트리를 베이스로 한 구현을 사용한다.

레드-블랙 트리의 조건

1. 모든 트리의 노드에 검은색 혹은 빨간색을 색칠한다.

2. 루트 노드는 항상 검은색이다.

3. 모든 리프 노드 들은 검은색이다.

4. 빨간색 노드의 자식은 양쪽 다 항상 검은색이다.

   4.1. 즉, 빨간색 노드는 연달아 나타날 수 없다.

   4.2. 이 규칙을 지키면, 검은색 노드만이 빨간색 노드의 부모가 될 수 있다.

5. 루트 노드에서 어떠한 자식 노드를 타고 가던지 리프 노드에 도달했을 때 항상 같은 수의 검은색 노드를 만나게 된다.

리프 노드 (leaf node) 란? 자식 노드가 더 이상 존재하지 않는 노드를 말한다. 리프의 뜻은 잎사귀이다. 더 뻗어나가는 가지가 아니라 잎사귀로 끝맺는 노드를 말한다.

리프 노드의 반대는 내부 노드(internal node) 라고 부른다.

레드-블랙 트리 삽입

• 레드 블랙 트리에서 모든 새로운 노드는 빨간색 색상을 가진채로 삽입되어야 한다.

  • 추후 레드-블랙 트리의 조건에 맞게 다시 변경한다.

    • 이 과정에서 재색칠, 회전 등이 일어난다.

• 삽입 연산에 드는 시간은 그냥 일반적인 이진 트리와 비슷하다.

• 삽입 연산 이후 레드-블랙 트리의 모든 조건을 체크해봐야 한다.

• 만일 모든 조건이 충족된다면, 다음 연산으로 넘어가고, 아니라면 아래와 같은 연산을 실행하여 레드-블랙 트리로 만들어주어야 한다.

  • 재색칠

  • 회전

  • 재색칠 이후 회전

레드-블랙 트리 삽입 절차

1. 트리가 비었는지 확인한다.

   1. 트리가 비었다면, 검은색 루트 노드를 삽입한다.

   2. 트리가 비어있지 않다면, 빨간색 리프 노드를 삽입한다.

      1. 새 노드의 부모가 검은색이라면, 연산을 마친다.

      2. 새 노드의 부모가 빨간색이면, 새 노드의 부모의 형제를 확인한다.

         1. 새 노드 부모의 형제가 검은색 혹은 NULL이면, 적절한 회전과 재색칠을 한다.

         2. 새 노드 부모의 형제가 빨간색이면, 재색칠을 한다.

간단한 의사코드 작성

if 트리가 비었는가?
  검은색 루트 노드 삽입 // 1.1
else
  새로운 빨간색 리프 노드 삽입 // 1.2
    if 새로운 빨간색 리프 노드의 부모가 검은색이 아닌가?
      if 새로운 빨간색 리프 노드의 부모 노드의 형제가 검은색인가?
        회전과 재색칠을 한다. // 1.2.2.1
      else
        while 레드-블랙 트리의 조건을 만족하지 않는가?
          내 부모와 부모의 형제를 검은색으로 칠한다.
          부모의 부모를 빨간색으로 칠한다. // 5. 조건을 맞추기 위함
          // 1.2.2.2

연산 종료 // 나머지 모두

/**
* T: 트리
* z: 새롭게 대입되는 값의 참조
* 이진트리에 의한 삽입 후에 레드 블랙 트리로 만드는 `RB_INSERT_FIXUP()` 함수를 통해 수정한다.
**/
RB_INSERT(T, z)
1  y <- nil[T] // 포인터 y에 트리의 nil을 넣는다.
2  x <- root[T] // 포인터 x에 트리의 루트 노드의 주소를 넣는다.
3  while x != nil[T] // 포인터 x가 nil이 아니라면, 계속 반복
4    do y <- x // y에 x를 대입 (시작 시점에는 y에 루트 노드의 참조가 대입)
5      if key[z] < key[x] // z의 key가 x의 key보다 작다면
6        then x <- left[x] // x에 x의 left(왼쪽 자식)를 대입함
7      else // z의 key가 x의 key보다 크다면
8        then x <- right[x] // x에 x의 right(오른쪽 자식)을 대입함
9  // x에는 결국 nil이 들어가고, y에는 x의 부모가 들어갈 것이다.
10 p[z] <- y // z의 부모에 y를 대입
11 if y = nil[T] // 부모가 들어가야 할 y가 트리의 nil이라면 (루트가 nil인 경우, x가 애초에 nil이라 while을 안탔을 때)
12   then root[T] <- z // 새로 들어온 값인 z가 트리의 루트 노드가 된다.
13   else if key[z] < key[y] // z의 key가 y의 key보다 작다면,
14          then left[y] <- z // y의 left에 z를 넣음
15          else right[y] <- z // z의 key가 y의 key보다 크다면, y의 right에 z를 넣음
16 left[z] <- nil[T] // 새롭게 들어간 z의 양쪽 자식에 nil을 넣어줌 (1)
17 right[z] <- nil[T] // 새롭게 들어간 z의 양쪽 자식에 nil을 넣어줌 (2)
18 color[z] <- RED // 새롭게 들어간 z의 color에 RED 값을 줌
19 RB_INSERT_FIXUP(T, z) // RED-BLACK TREE에 맞게 고치는 함수 실행

/**
* T: 트리
* z: 새롭게 대입되는 값의 참조
* 이진트리의 규칙에 의해 새롭게 트리에 노드가 추가된 이후에도 레드-블랙 트리의 규칙이 지켜지게 만드는 함수
**/
RB-INSERT-FIXUP(T, z)
1  while color[p[z]] = RED // 
2    do if p[z] = left[p[p[z]]]
3        then y <- right[p[p[z]]]
4          if color[y] = RED
5            then color[p[z]] <- BLACK   // CASE 1
6                 color[y] <- BLACK      // CASE 1
7                 color[p[p[z]]] <- RED  // CASE 1
8                 z <- p[p[z]]           // CASE 1
9          else if z = right[p[z]]
10                then z <- p[z]         // CASE 2
11                     LEFT-ROTATE(T, z) // CASE 2
12              color[p[z]] <- BLACK     // CASE 3
13              color[p[p[z]]] <- RED    // CASE 3
14              RIGHT-ROTATE(T, p[p[z]]) // CASE 3
15      else(same as then clause with "right" and "left" exchanged)
16 color[root[T]] <- BLACK

/**
* T: 트리
* z: 새롭게 대입되는 값의 참조
* RB-INSERT_FIXUP을 도와주는 좌측 회전 함수
**/
LEFT-ROTATE(T, x)
01  y <- right[x]        //Set y
02  right[x] <- left[y]  //Turn y's left subtree into x's right 
03  p[left[y]] <- x
04  p[y] <- p[x]         //Link x's parent to y
05  if p[x] = NIL[T]
06    then root[T] <- y
07    else if x = left[p[x]]
08      then left[p[x]] <- y
09      else right[p[x]] <- y
10  left[y] <- x         //Put x on y's left
11  p[x] <- y

자바 코드 구현

package com.company.red_black_tree;

public class RedBlackTreeTest {
    private static final int BLACK = 0;
    private static final int RED = 1;

    private static Node root;

    private static class Node {
        private int value;
        private int color;

        Node left;
        Node right;
        Node parent;

        Node(int value) {
            this.value = value;
            color = BLACK;

            left = null;
            right = null;
            parent = null;
        }

        Node() {
            this(-1);
        }

        int getValue() {
            return value;
        }

        String getColor() {
            return color == RED ? "RED" : "BLACK";
        }

        void setColor(int color) {
            this.color = color;
        }
    }

    private static void printTree(Node node) {
        if (node == null)
            return;

        System.out.println(node.getValue() + "(" + node.getColor() + ")");
        printTree(node.left);
        printTree(node.right);
    }

    private static Node findNode(Node goal, Node node) {
        if(node == null)
            return null;

        if(goal.getValue() < node.getValue()) {
            if(node.left != null)
                return findNode(goal, node.left);
        }

        else if(goal.getValue() > node.getValue()) {
            if(node.right != null)
                return findNode(goal, node.right);
        }

        else {
            return node;
        }

        return null;
    }

    public static void insertNode(Node node) {
        System.out.println("Inserted " + node.getValue());

        // 트리가 비었는지 확인
        if(root == null) {
            // 루트가 없는 경우, 검은색 루트 노드를 새로 만들며 시작 (조건 1.1.)
            node.setColor(BLACK);
            root = node;
        }
        else {
            // 루트 노드가 있는 경우, 빨간색 리프 노드를 삽입 (조건 1.2.)
            node.setColor(RED);
            Node parent = root;


            // 기본 이진트리 규칙대로 노드 추가하기 (빨간색 리프 노드의 자리 찾기)
            while(true) {
                // 노드의 값이 부모보다 크다면 계속 오른쪽 자식을 부모로 접근
                if(node.getValue() > parent.getValue()) {
                    // 부모의 오른쪽 자식 자리가 비었다면, 오른쪽 자식이 됨
                    if(parent.right == null) {
                        parent.right = node;
                        node.parent = parent;
                        break;
                    }
                    else {
                        // 트리에서 한줄기 오른쪽으로 내려와서 빈공간 찾기 (while)
                        parent = parent.right;
                    }
                }
                // 노드의 값이 부모보다 작다면 계속 왼쪽 자식을 부모로 접근
                else {
                    // 부모의 왼쪽 자식 자리가 비었다면, 왼쪽 자식이 됨
                    if(parent.left == null) {
                        parent.left = node;
                        node.parent = parent;
                        break;
                    } else {
                        // 트리에서 한줄기 왼쪽으로 내려와서 빈공간 찾기 (while)
                        parent = parent.left;
                    }
                }
            }

            // 새 노드의 부모가 빨간색일 때만 새 노드의 부모의 형제 확인 및 재색칠, 회전 적용 (조건 1.2.2.)
            if(node.parent != null && "RED".equals(node.parent.getColor())){
                recolorTree(node);
            }
        }
    }

    public static void recolorTree(Node node) {
        System.out.println("RedBlackTreeTest.recolorTree");

        // 부모의 색이 빨간색이 아닐 때까지 재색칠을 할 것이다.
        while (node.parent != null && "RED".equals(node.parent.getColor())) {
            Node siblingOfParent = null;

            // 해당 노드 부모가 조부모 노드의 왼쪽노드 자식이라면 (회전 방향 정하기)
            if(node.parent == node.parent.parent.left) {
                // 부모의 형제는 부모의 부모의 오른쪽노드 자식이다. (부모는 왼쪽 노드 자식이기 때문)
                siblingOfParent = node.parent.parent.right;

                // 부모의 형제가 빨간색이라면 (1.2.2.2)
                if(siblingOfParent != null && "RED".equals(siblingOfParent.getColor())) {
                    node = whenSiblingOfParentIsRed(node, siblingOfParent);
                    continue;
                }

                // 내 부모의 형제가 검은색이라면 (1.2.2.1) -> 회전 + 재색칠
                else {
                    // 내가 부모 기준 우측에 있는 자식이라면, 좌측 회전
                    if(node == node.parent.right) {
                        node = node.parent;
                        rotateLeft(node);
                    }

                    // 부모의 색이 빨간색인 것이 실행 조건이었으니,
                    // 내 부모의 색은 검은색을 만들어줌 (재색칠)
                    node.parent.setColor(BLACK);
                    // 내 부모의 부모는 빨간색이 됨 (재색칠)
                    node.parent.parent.setColor(RED);

                    // 내 부모의 부모를 우측 회전시키기
                    rotateRight(node.parent.parent);
                    break;
                }
            }

            // 내 부모가 / 조부모 노드의 오른쪽 자식이라면 (회전 방향 정하기)
            else {
                // 부모 노드의 형제는 부모 노드의 부모 노드의 왼쪽 자식이다. (부모는 오른쪽 노드 자식이기 때문)
                siblingOfParent = node.parent.parent.left;

                // 내 부모의 형제가 빨간색이라면 (1.2.2.2)
                if(siblingOfParent != null && "RED".equals(siblingOfParent.getColor())) {
                    node = whenSiblingOfParentIsRed(node, siblingOfParent);
                    continue;
                }

                // 내 부모의 형제가 검은색이라면 (1.2.2.1) -> 회전 + 재색칠
                else {
                    // 내가 부모 기준 좌측에 있는 자식이라면, 우측 회전
                    if(node == node.parent.left) {
                        node = node.parent;
                        rotateRight(node);
                    }

                    // 부모의 색이 빨간색인 것이 실행 조건이었으니,
                    // 내 부모의 색은 검은색을 만들어줌 (재색칠)
                    node.parent.setColor(BLACK);
                    // 내 부모의 부모는 빨간색이 됨 (재색칠)
                    node.parent.parent.setColor(RED);

                    // 내 부모의 부모를 좌측 회전시키기
                    rotateLeft(node.parent.parent);
                    break;
                }
            }
        }

        root.setColor(BLACK);
    }

    public static Node whenSiblingOfParentIsRed(Node node, Node siblingOfParent) {
        // 부모를 검정으로 만듦 (부모의 형제가 빨간색인 것이 밝혀졌으니, 부모도 빨간색일 것임)
        node.parent.setColor(BLACK);
        // 부모의 형제도 검정으로 만듦
        siblingOfParent.setColor(BLACK);
        // 부모의 부모는 빨강으로 만듦 (이래야 5. 조건이 만족됨)
        node.parent.parent.setColor(RED);

        //부모의 부모를 반환하고, 다시 반복해서 부모의 부모의 부모가 또 빨간색이면 같은 행위(재색칠)를 반복해야 함
        return node.parent.parent;
    }

    private static void rotateLeft(Node node) {
        System.out.println("RedBlackTreeTest.rotateLeft");

        // 부모가 존재하지 않을 때
        if(node.parent == null) {
            Node right = root.right;
            root.right = root.right.left;
            right.left = new Node();
            right.left.parent = root;
            root.parent = right;
            right.left = root;
            right.parent = null;
            root = right;
        }

        // 부모가 존재한다면,
        else {
            // 해당 노드가 왼쪽 자식이라면 (해당 노드가 부모 노드보다 작다면)
            // 해당 노드의 오른쪽 자식은 해당 노드보다 크지만, 부모 노드보다는 작음
            if(node == node.parent.left) {
                node.parent.left = node.right;
            }
            // 해당 노드가 오른쪽 자식이라면 (해당 노드가 부모 노드보다 크다면)
            // 해당 노드의 오른쪽 자식도 해당 노드의 부모보다 큼
            else {
                node.parent.right = node.right;
            }

            node.right.parent = node.parent;
            node.parent = node.right;

            if(node.right.left != null) {
                node.right.left.parent = node;
            }

            node.right = node.right.left;
            node.parent.left = node;
        }
    }

    private static void rotateRight(Node node) {
        System.out.println("RedBlackTreeTest.rotateRight");

        if(node.parent == null) {
            Node left = root.left;
            root.left = root.left.right;
            left.right = new Node();
            left.right.parent = root;
            root.parent = left;
            left.right = root;
            left.parent = null;
            root = left;
        }

        // 부모가 존재한다면,
        else {
            // 해당 노드가 왼쪽 자식이라면 (해당 노드가 부모 노드보다 작다면)
            // 해당 노드의 왼쪽 자식도 부모 노드보다 작음
            if(node == node.parent.left) {
                node.parent.left = node.left;
            }
            // 해당 노드가 오른쪽 자식이라면 (해당 노드가 부모 노드보다 크다면)
            // 해당 노드의 왼쪽 자식도 부모 노드보다 큼
            // (조부모 노드보다 작았다면 조부모노드의 왼쪽 방향에 삽입되어야 하기 때문)
            else {
                node.parent.right = node.left;
            }

            node.left.parent = node.parent;
            node.parent = node.left;

            if(node.left.right != null) {
                node.left.right.parent = node;
            }

            node.left = node.left.right;
            node.parent.right = node;
        }
    }

    public static void main(String[] args) {
        root = null;
        insertNode(new Node(8));
        insertNode(new Node(18));
        insertNode(new Node(5));
        insertNode(new Node(15));
        insertNode(new Node(17));
        insertNode(new Node(25));
        insertNode(new Node(40));
//        insertNode(new Node(80));

        System.out.println();
        printTree(root);
    }
}

예제 (Step by step)

8, 18, 5, 15, 17, 25, 40을 삽입해보겠다.

8 삽입

레드-블랙 트리 삽입 절차에서 1. 항목에 의해 트리가 비어있음을 확인하였고, 1.1. 항목에 의해 검은색 루트 노드를 삽입했다.

18 삽입

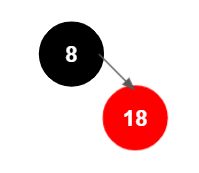
이진트리 기본 규칙에 의해 부모 노드보다 크므로 오른쪽에 삽입된다. 레드-블랙 트리 삽입 절차의 1.2의 규칙에 따라 빨간색 리프 노드가 삽입되었고 1.2.1의 규칙에 따라 부모가 검은색이므로 연산을 마친다.

5 삽입

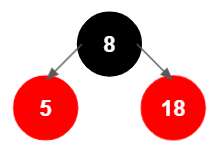
이진트리의 기본 규칙에 의해 부모 노드보다 작으므로 왼쪽에 삽입된다. 나머지는 18을 삽입할 때와 동일한 규칙이 적용되었다.

15 삽입

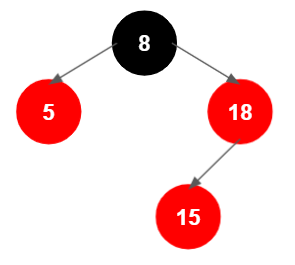
이진트리의 기본 규칙에 의해 루트 노드보다 크므로 오른쪽 아래로 그리고 18 노드보다는 작으므로 왼쪽 아래에 위치했다.

그런데, 위의 모습은 새 노드 부모(18)의 형제가 빨간색이므로, 삽입 절차 중 1.2.2.2에 해당한다. 그러므로 재색칠을 한다.

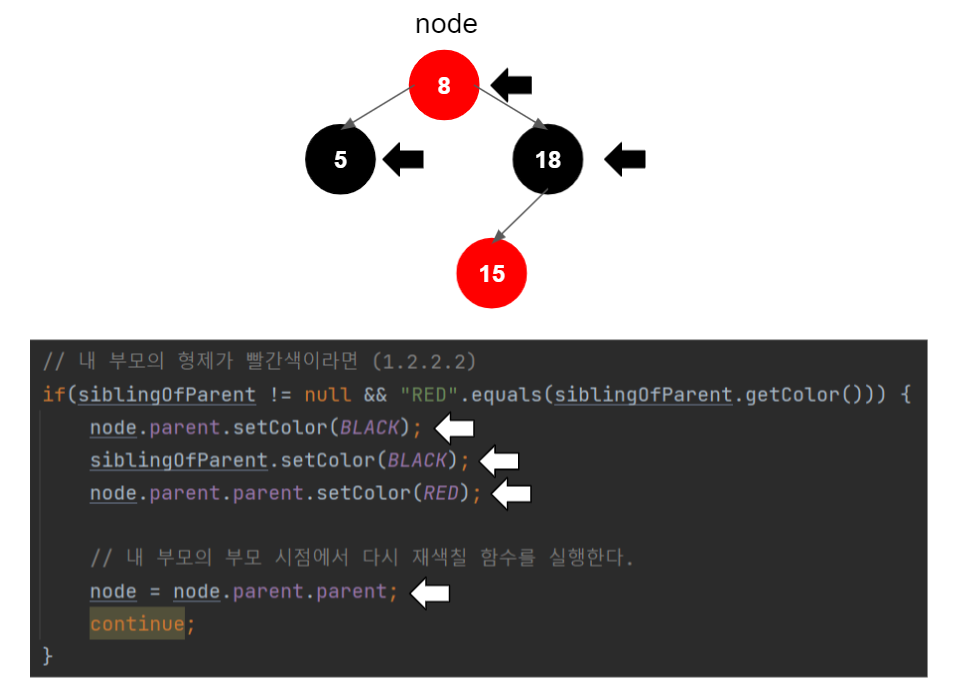
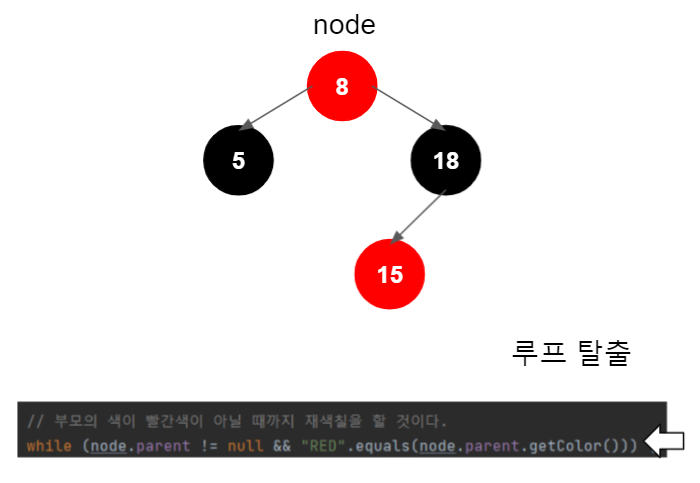
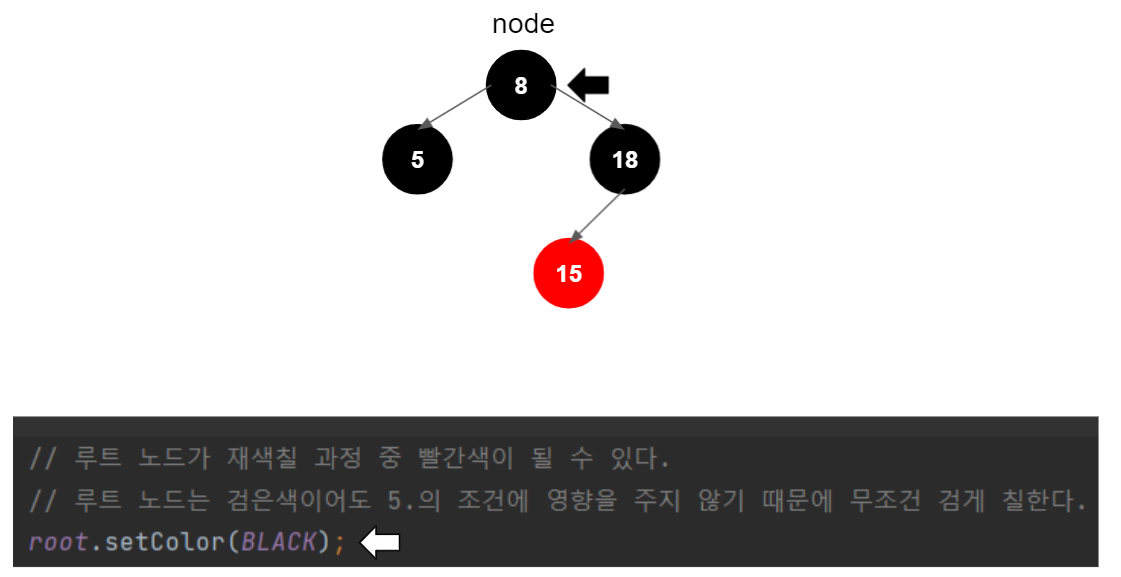
17 삽입

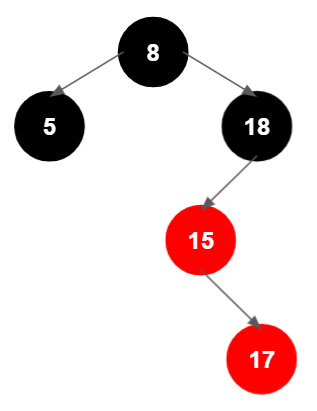
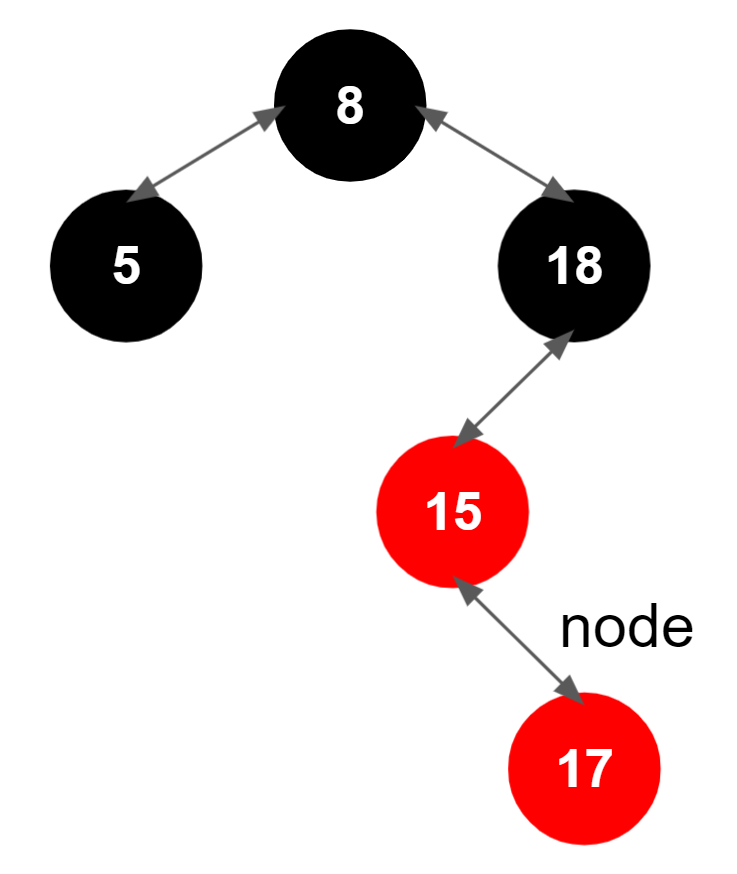
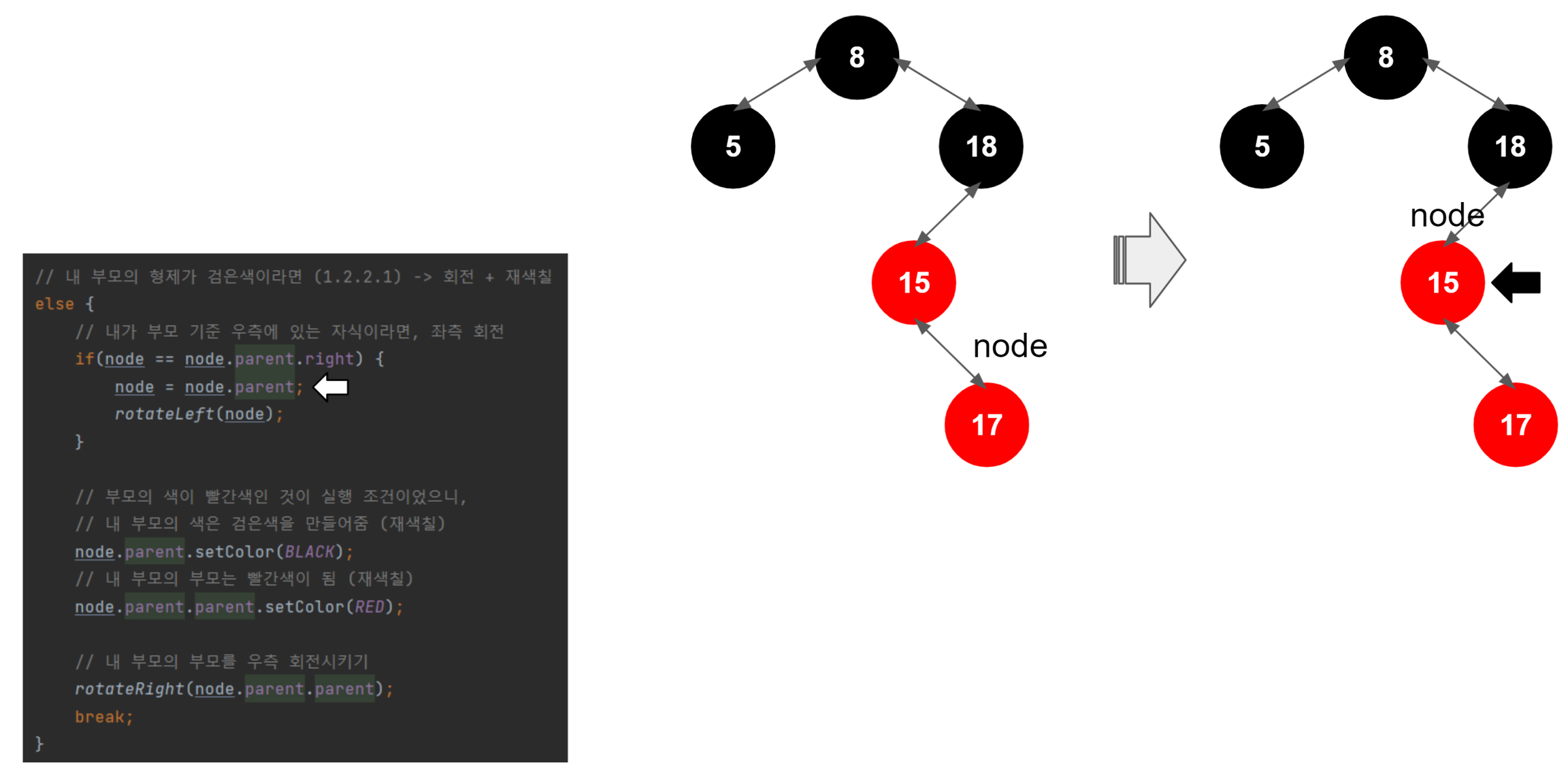
좌측 회전을 위해 먼저 해당 노드를 부모 노드로 설정함

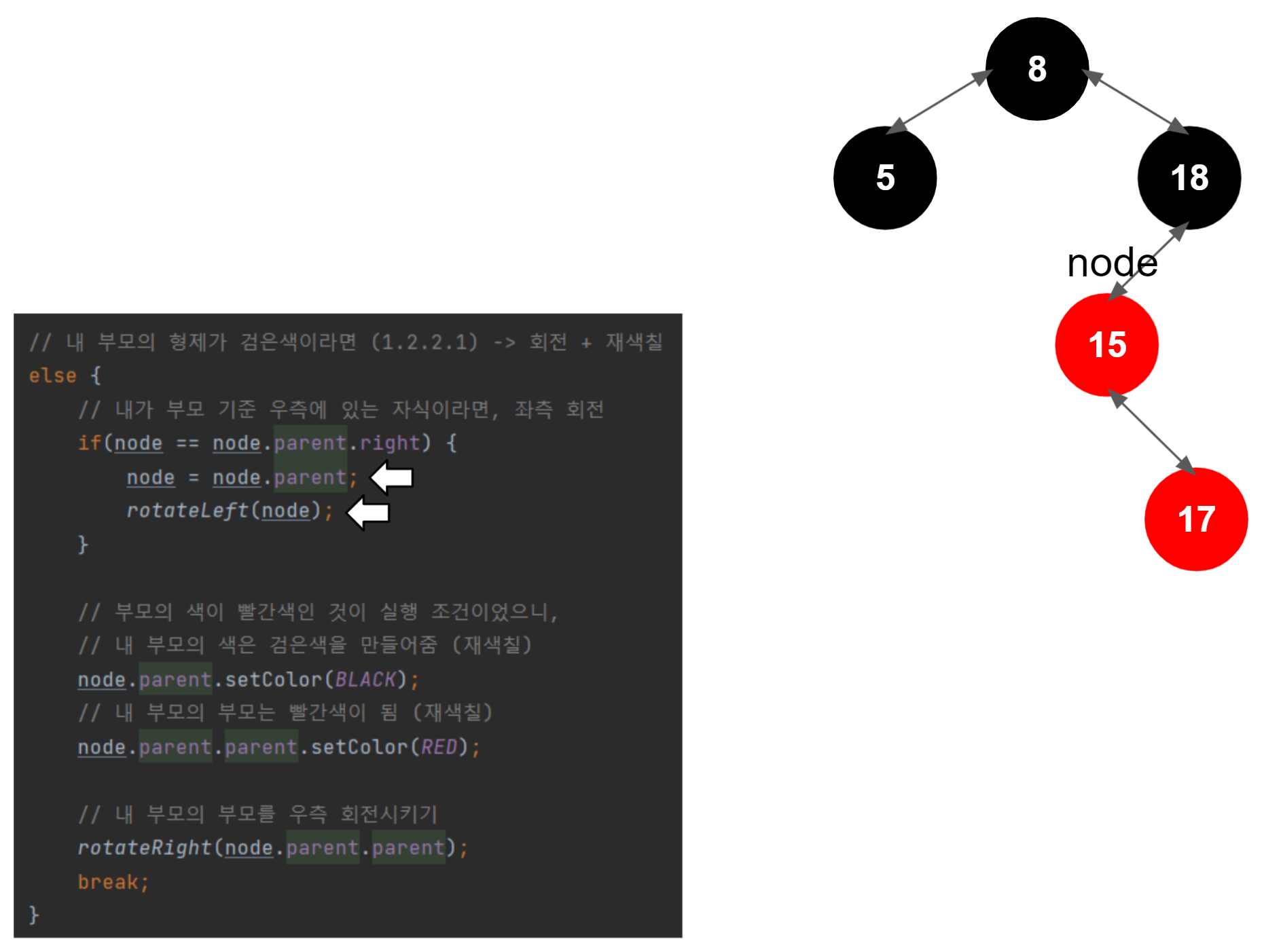
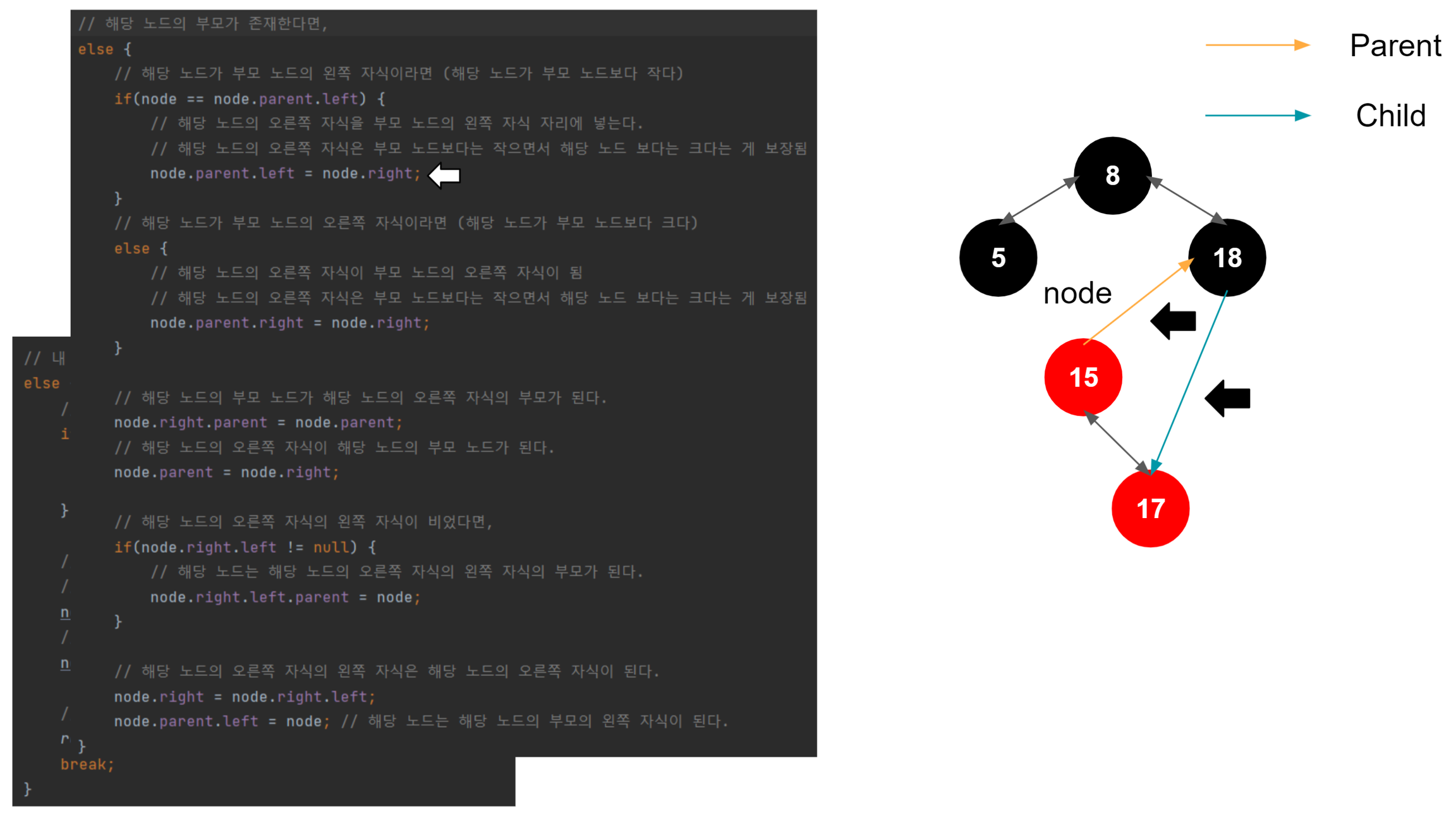
좌측 회전 시작

해당 노드가 왼쪽 자식일 때, 해당 노드의 왼쪽 자식이 부모의 왼쪽 자식이 된다. 이게 일어나는 이유는, 이진트리의 규칙을 따라서 삽입되었다고 가정했을 때, 1. 노드가 왼쪽 자식이라면 부모 노드보다 작다는 것이 보장된다. (부모 노드 > 노드) 2. 노드가 가진 오른쪽 자식은 노드보다는 크지만, 노드의 부모 노드보다는 작은 것이 보장된다. (부모 노드 > 노드의 오른쪽 자식 > 노드) 3. 결국 노드의 오른쪽 자식이 부모 노드의 왼쪽 자식으로 편입되어도 아무런 문제가 없다.

이러한 회전을 하는 이유는 결국 균형이 맞지 않게 주렁주렁 아래 노드로만 편입되는 현상을 막기 위함을 알아야 한다. 간단히 추상화하면, 부모, 해당 노드, 해당 노드의 자식 노드 총 3개의 노드가 있을 때 가운데 값을 위로 올려서 가운데 값을 기준으로 나머지 노드를 왼쪽 자식 노드로 오른쪽 자식 노드로 배치하여 트리의 height 를 줄이려는 것이다. (어떤 블로그에서는 이러한 행위를 회전(rotate) 이라고 표현하지 않고, 재구성(restructure) 이라고 표현하기도 한다.) 하지만 이번 좌측 회전이 끝나도 height 가 줄어들진 않고, 이후에 우측 회전에 끝난 후에는 height 가 1 감소할 것이다. 좌측 회전이 끝난 후에는 마지막 노드가 부모의 왼쪽 자식이 된다.

The height of a node is the length of the longest downward path to a leaf from that node. (height 란, 해당 노드로부터 리프 노드까지 내려가는 가장 긴 경로의 길이이다.)

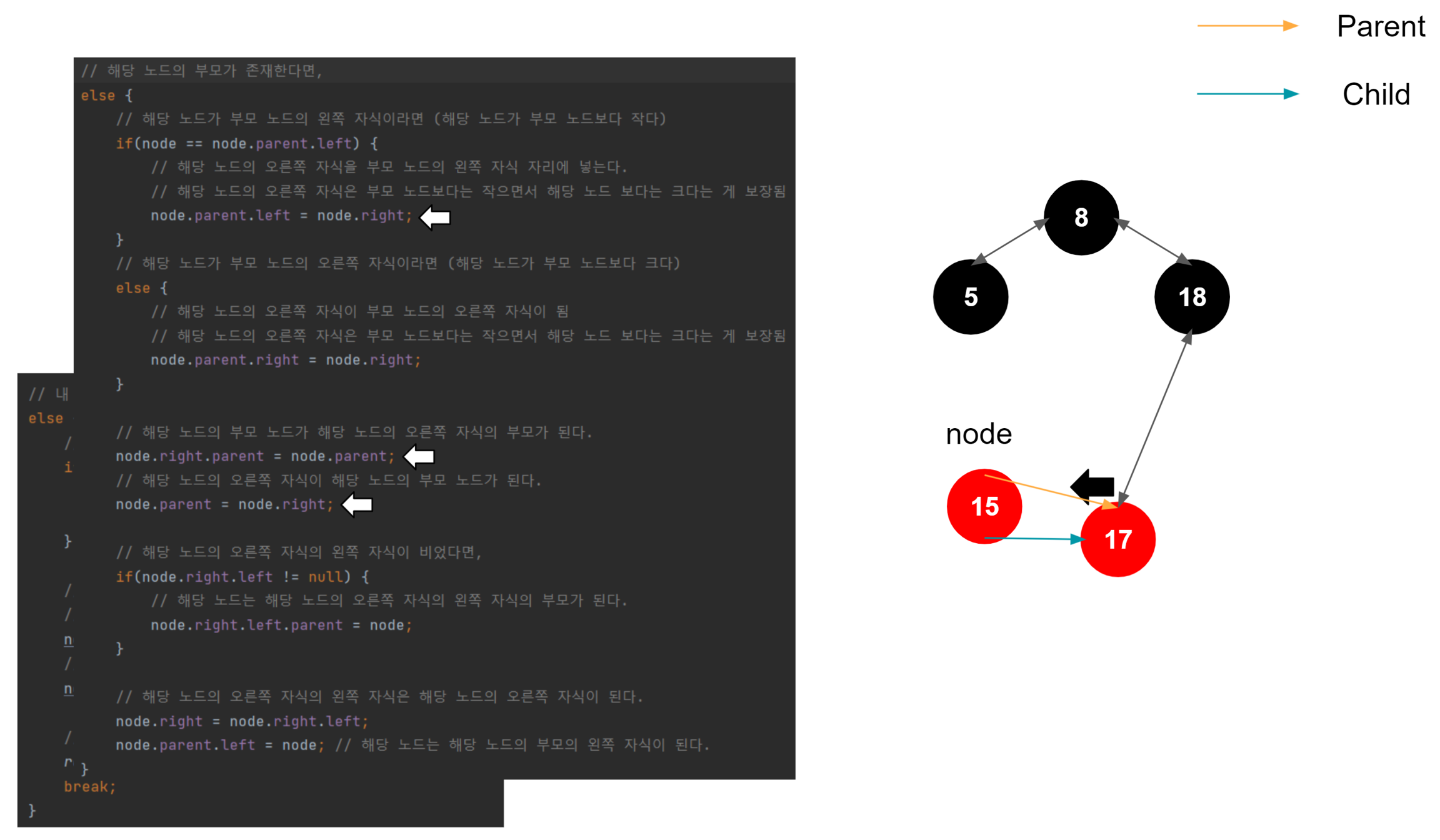
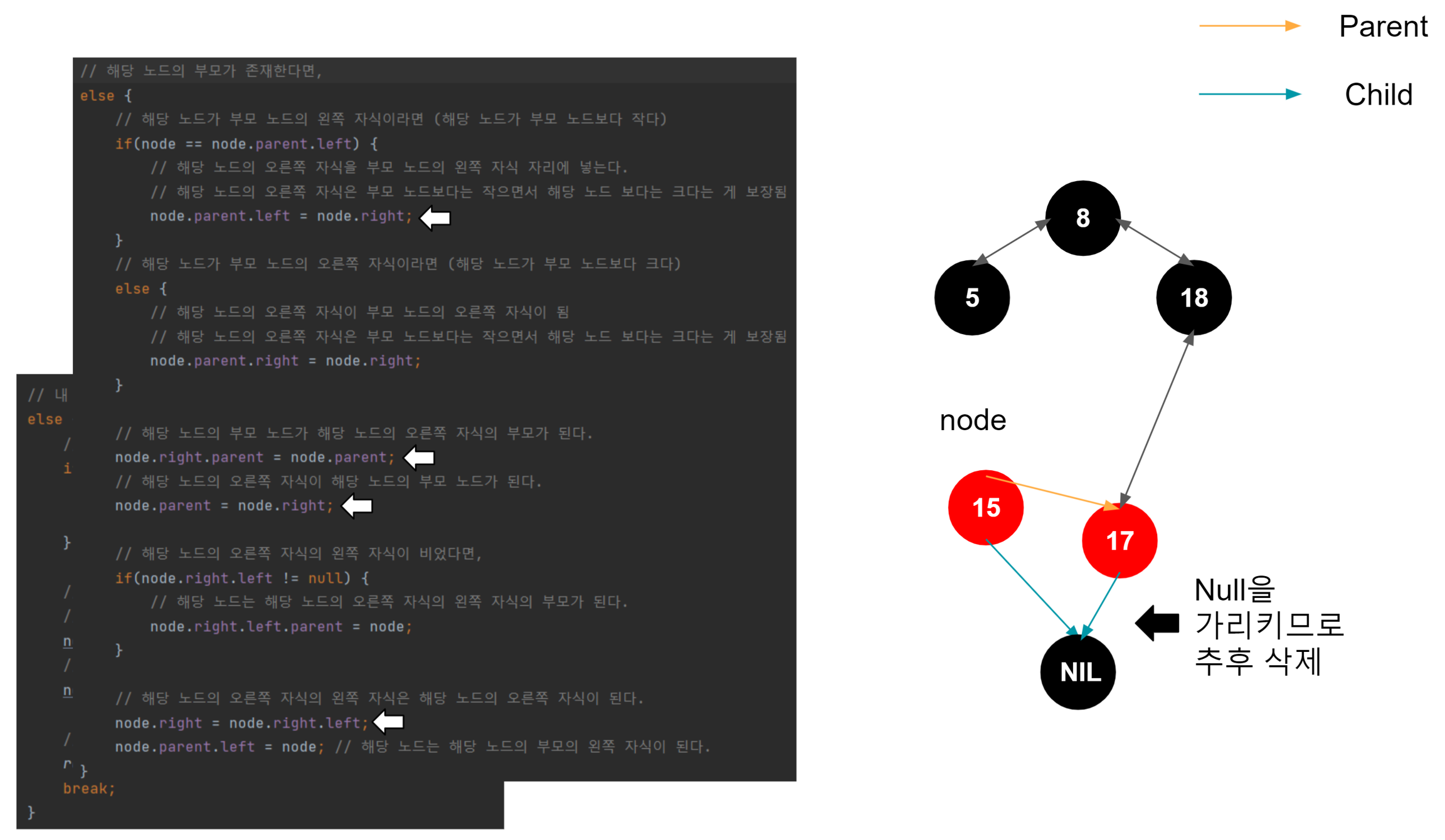
여기까지가 좌측 회전의 끝이다. 결과적으로 18과 가장 차이가 적게 나는 17이 왼쪽 자식 노드로 올라왔고, 15는 17의 자식 노드가 되었다.

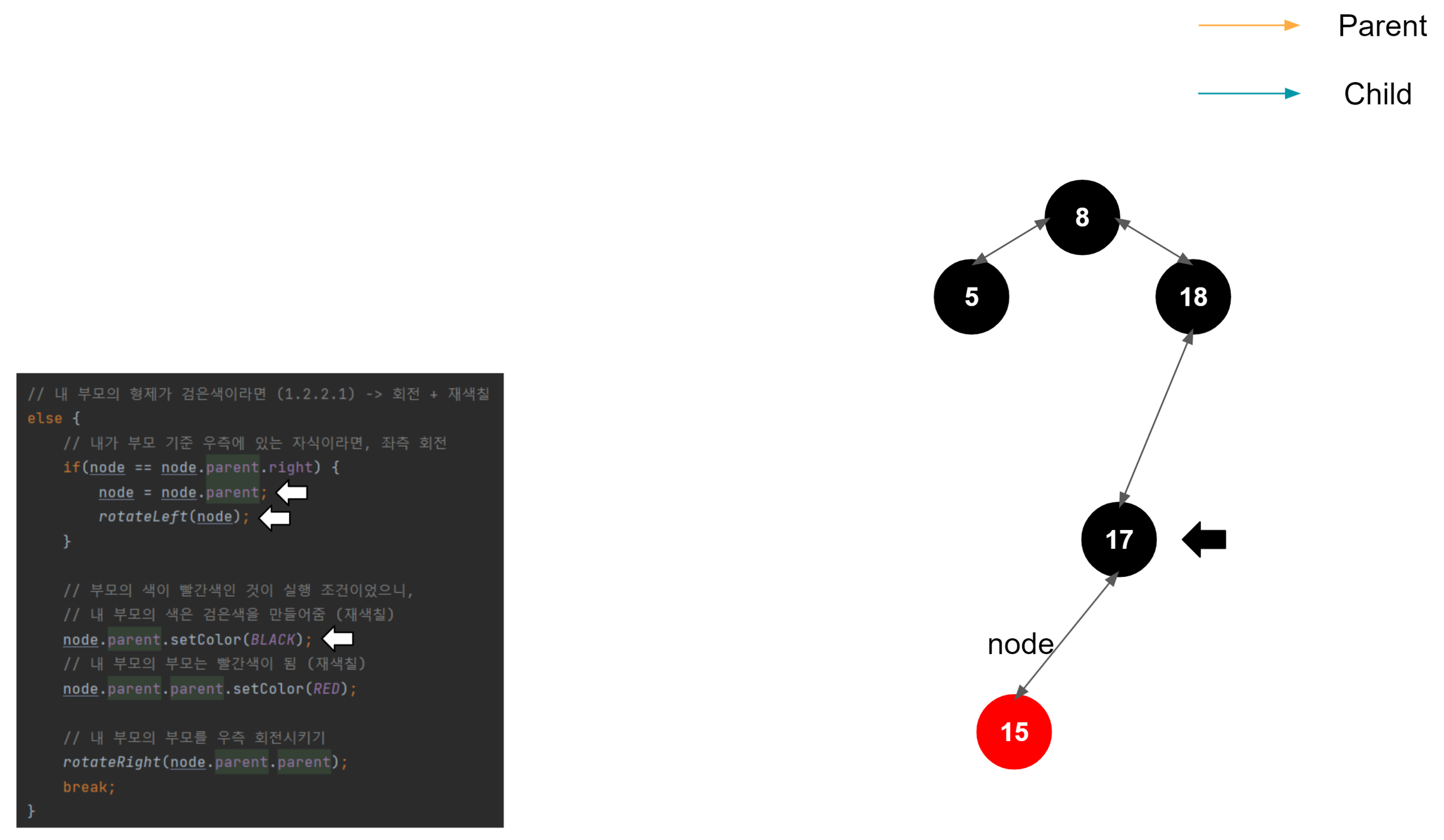
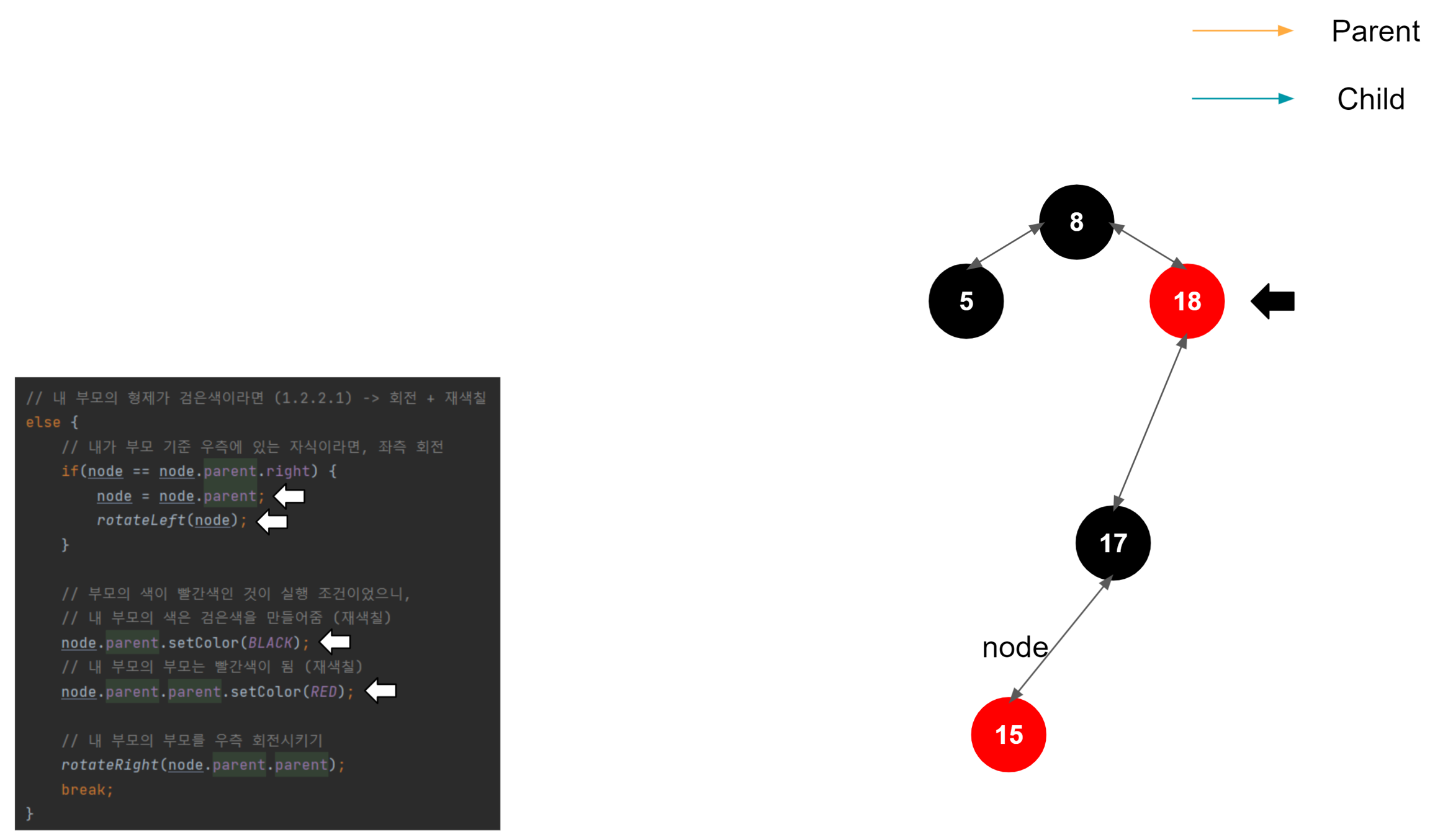
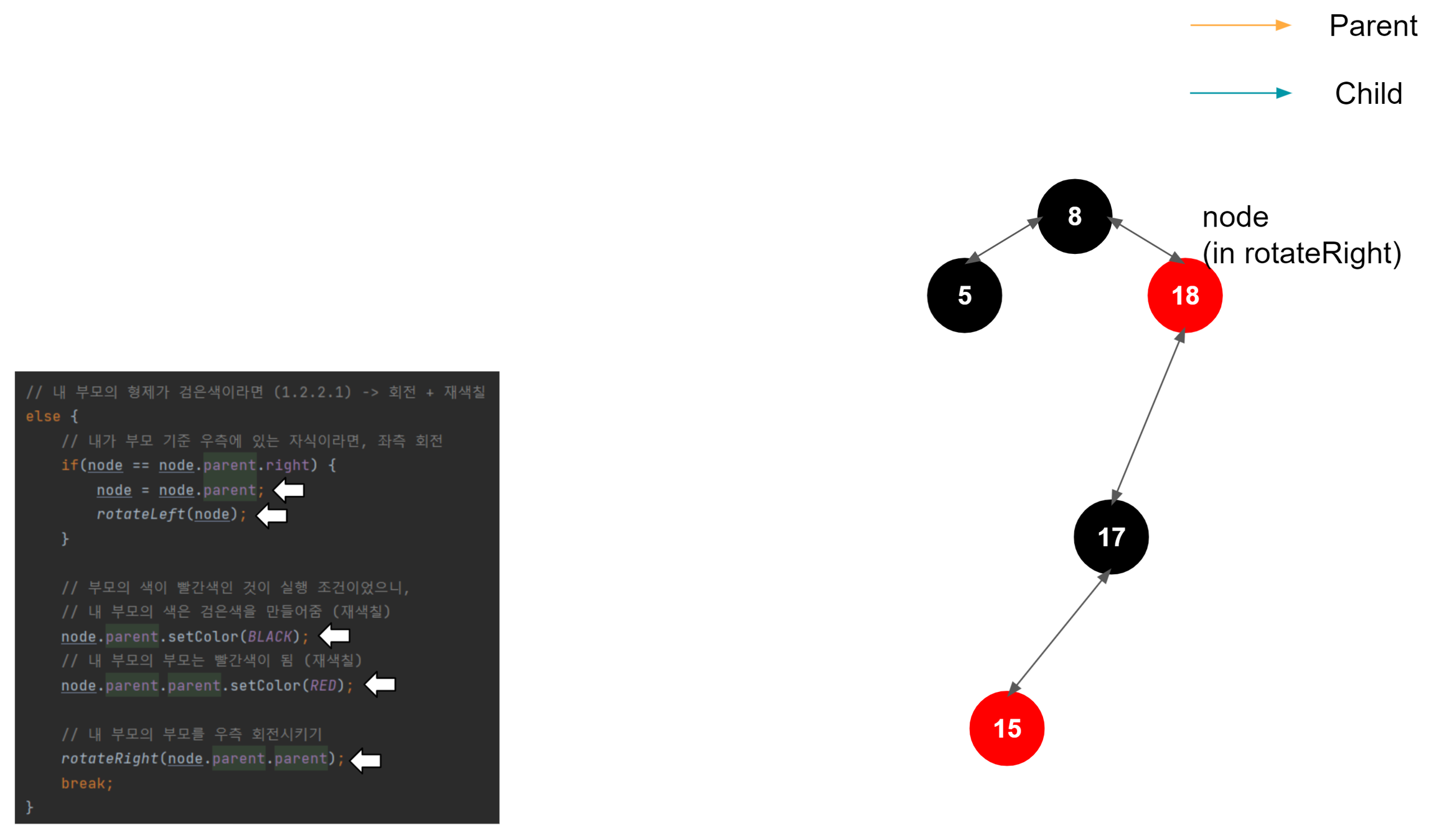
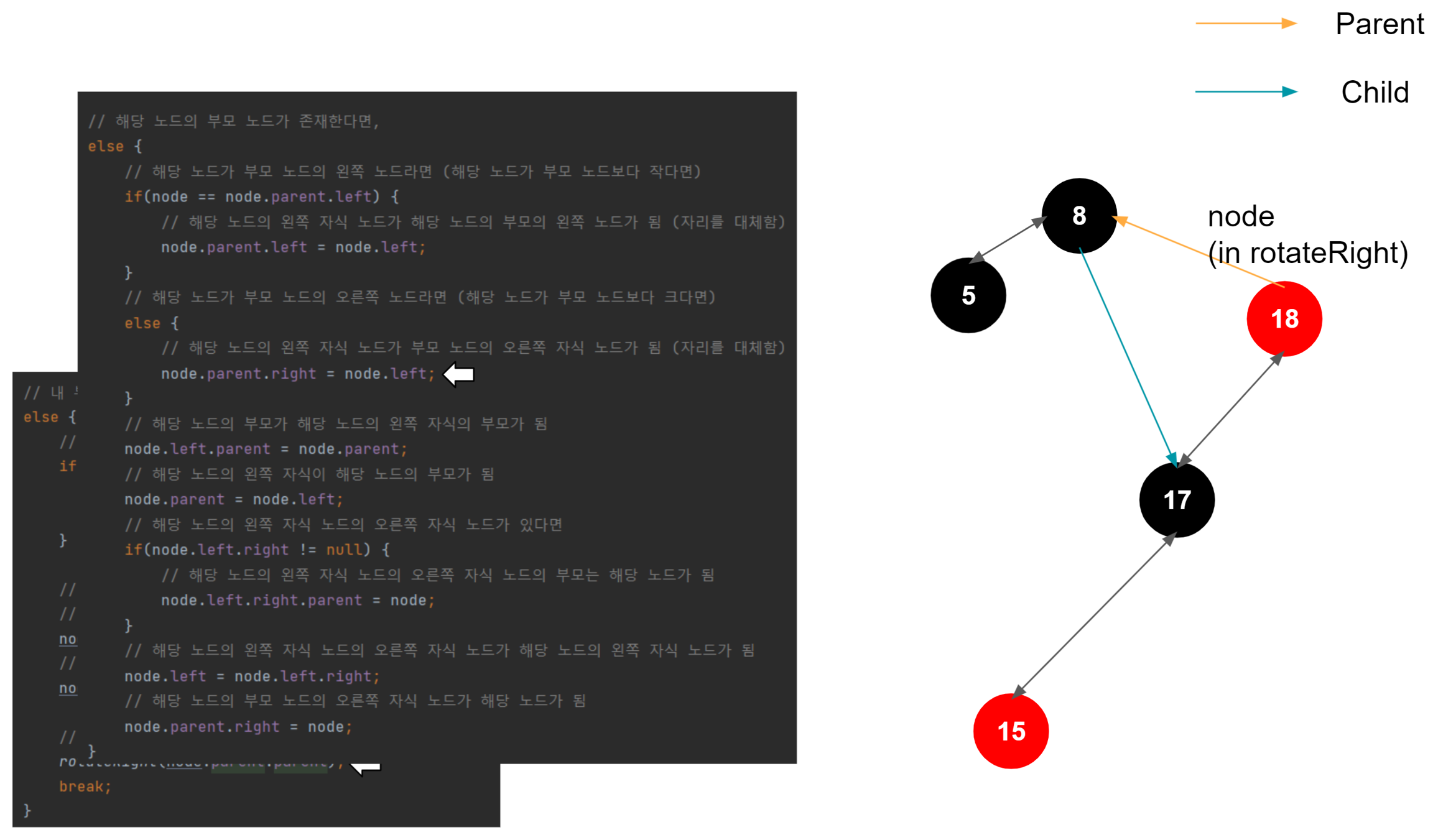
우측 회전 시작

우측 회전도 결국엔 좌측 회전과 매커니즘은 동일하다. 부모 노드, 노드, 자식 노드가 있을 때, 대소 관계를 비교한다. 여기서는 회전을 주체하는 해당 노드가 우측 노드이므로, 노드 > 자식 노드 > 부모 노드의 관계가 성립한다. 그러므로 중간 값인 자식 노드를 위로 올려 밸런스를 맞추는 로직이 진행된다.

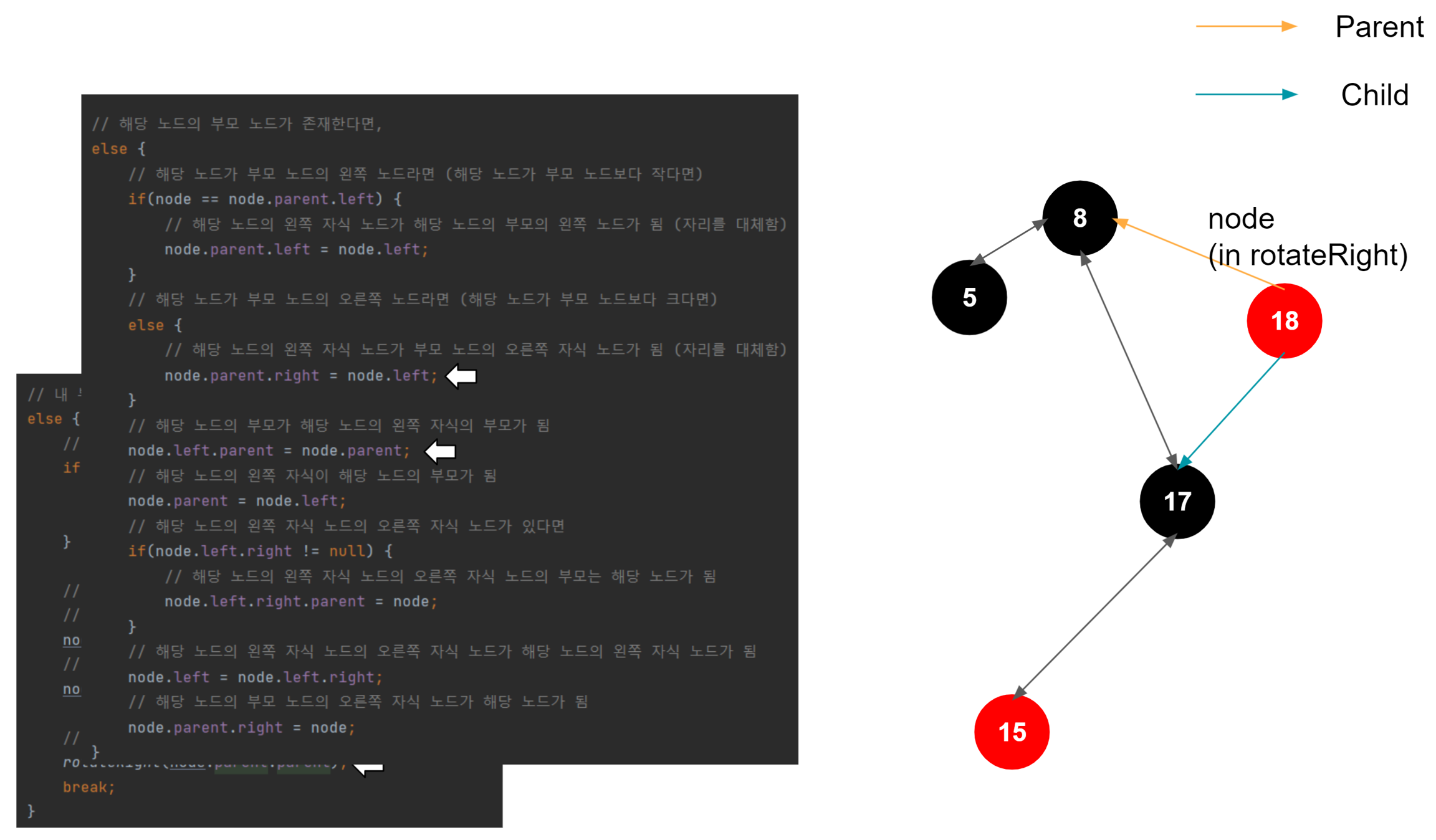
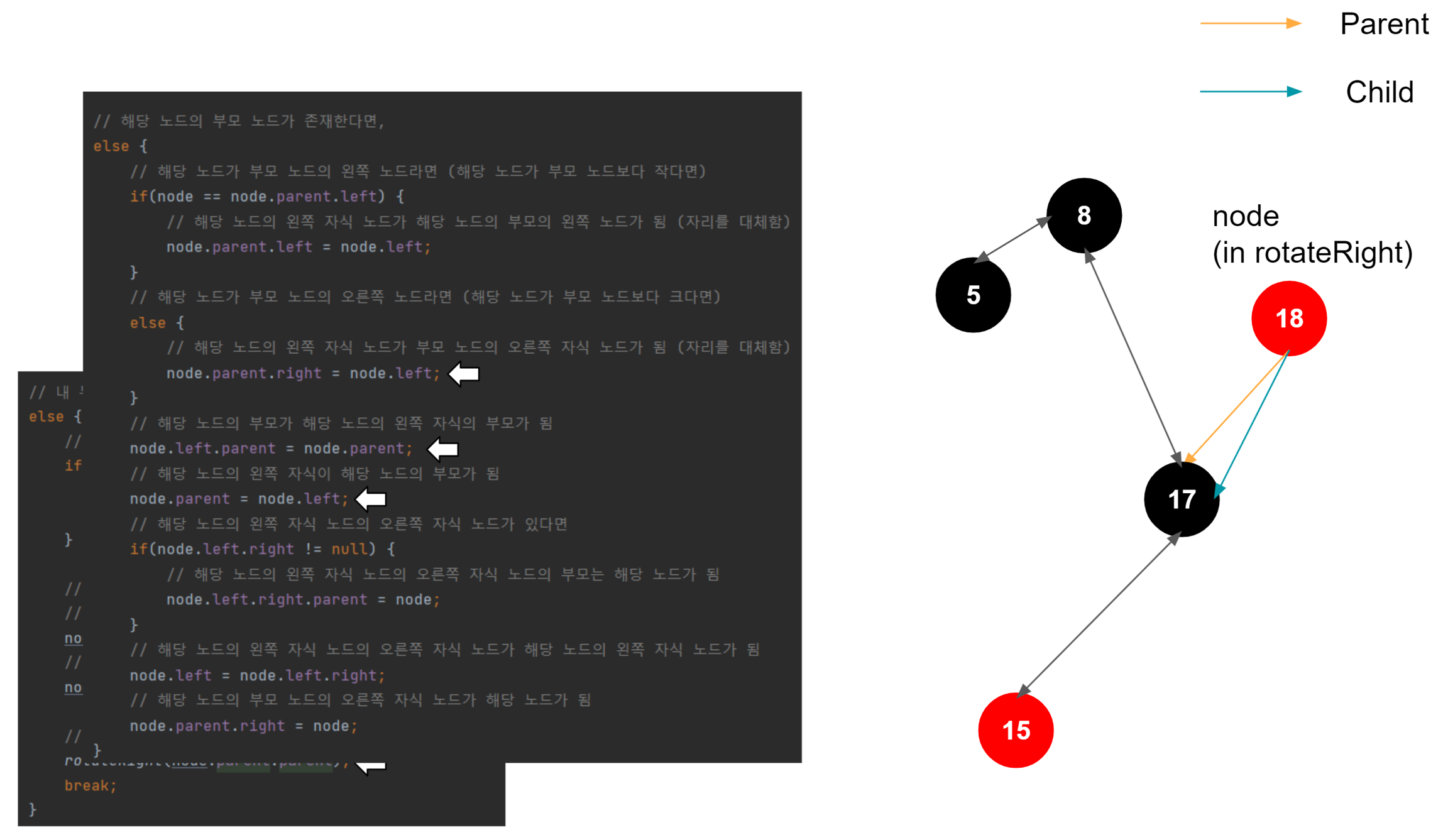
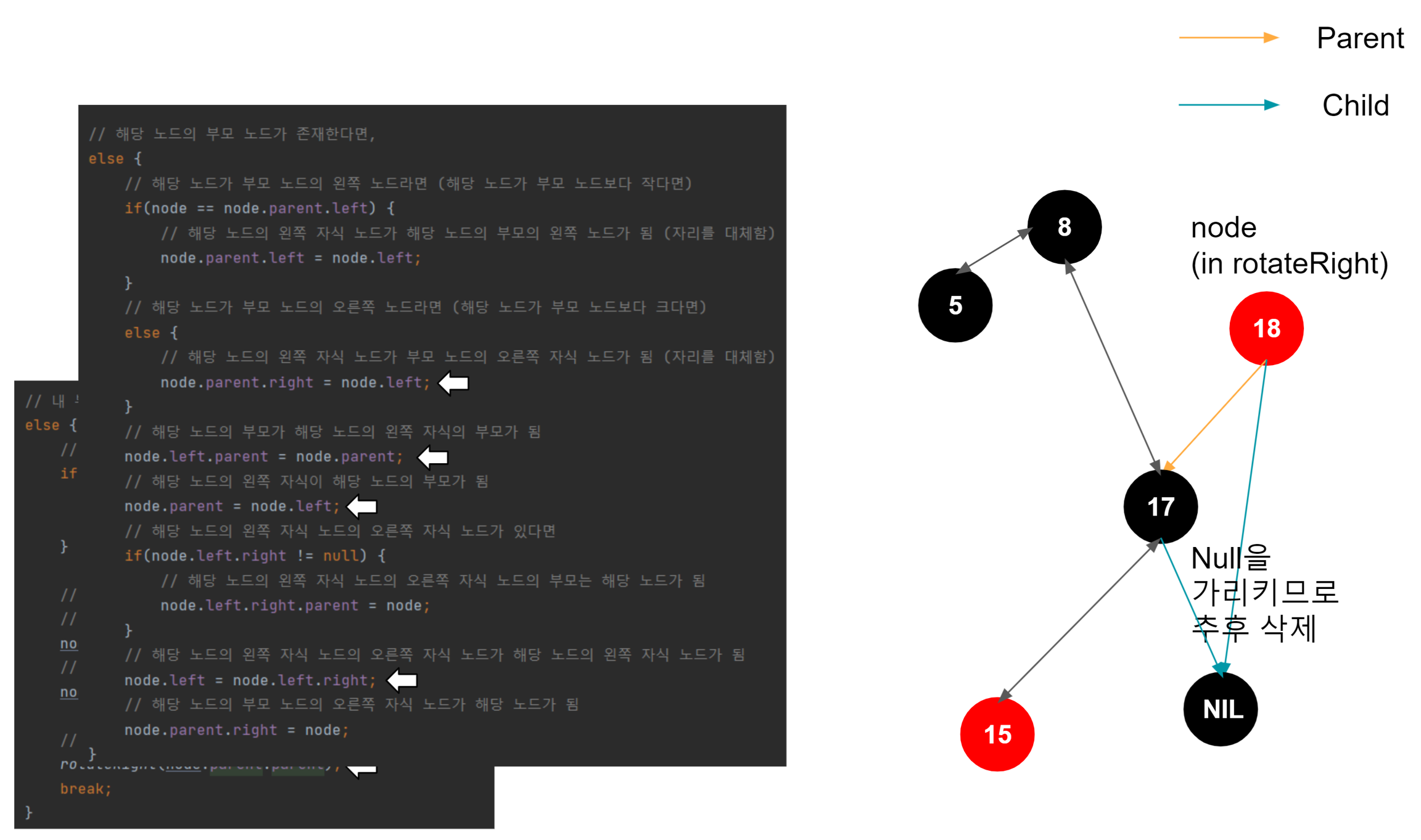
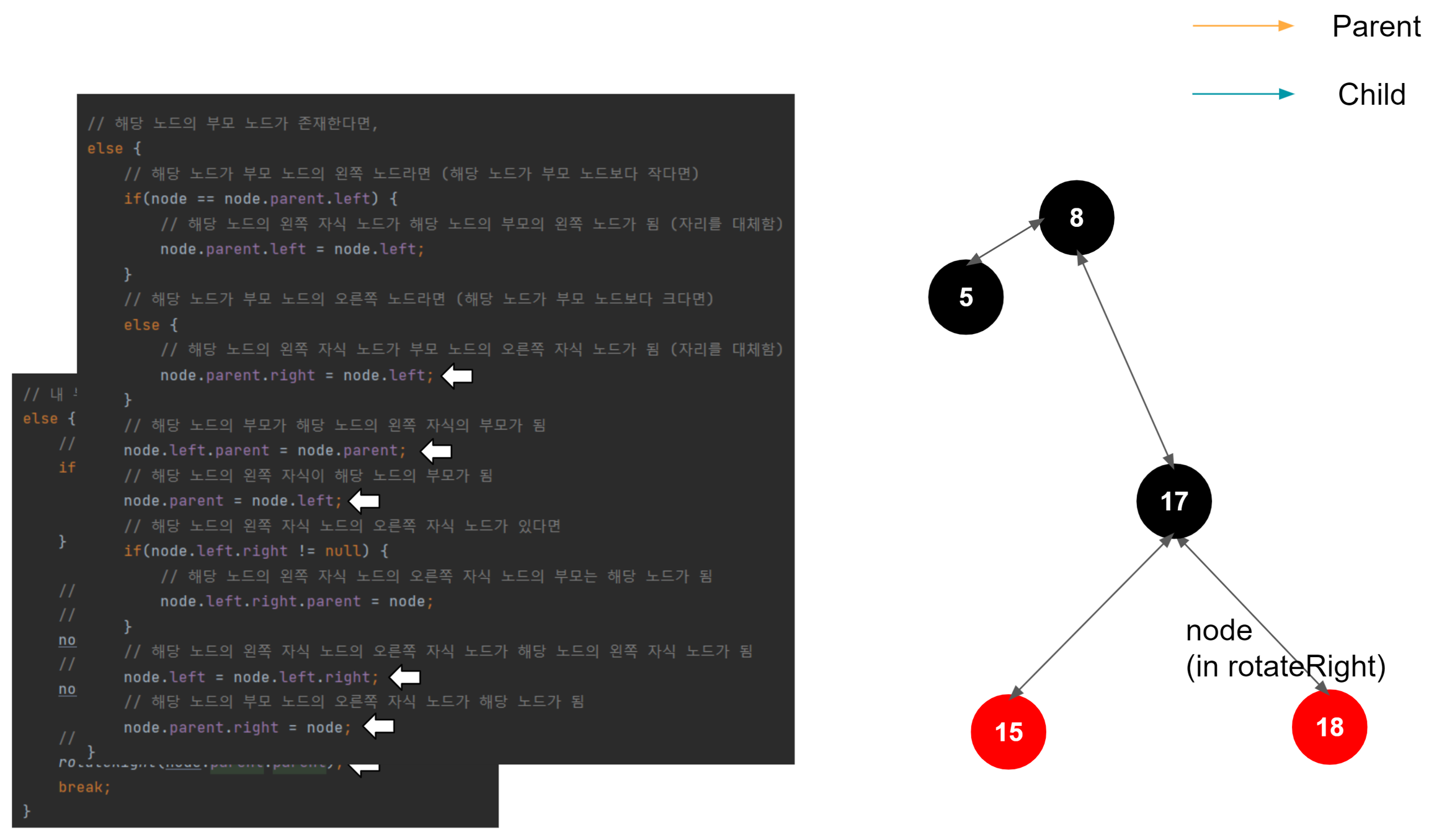
25 삽입

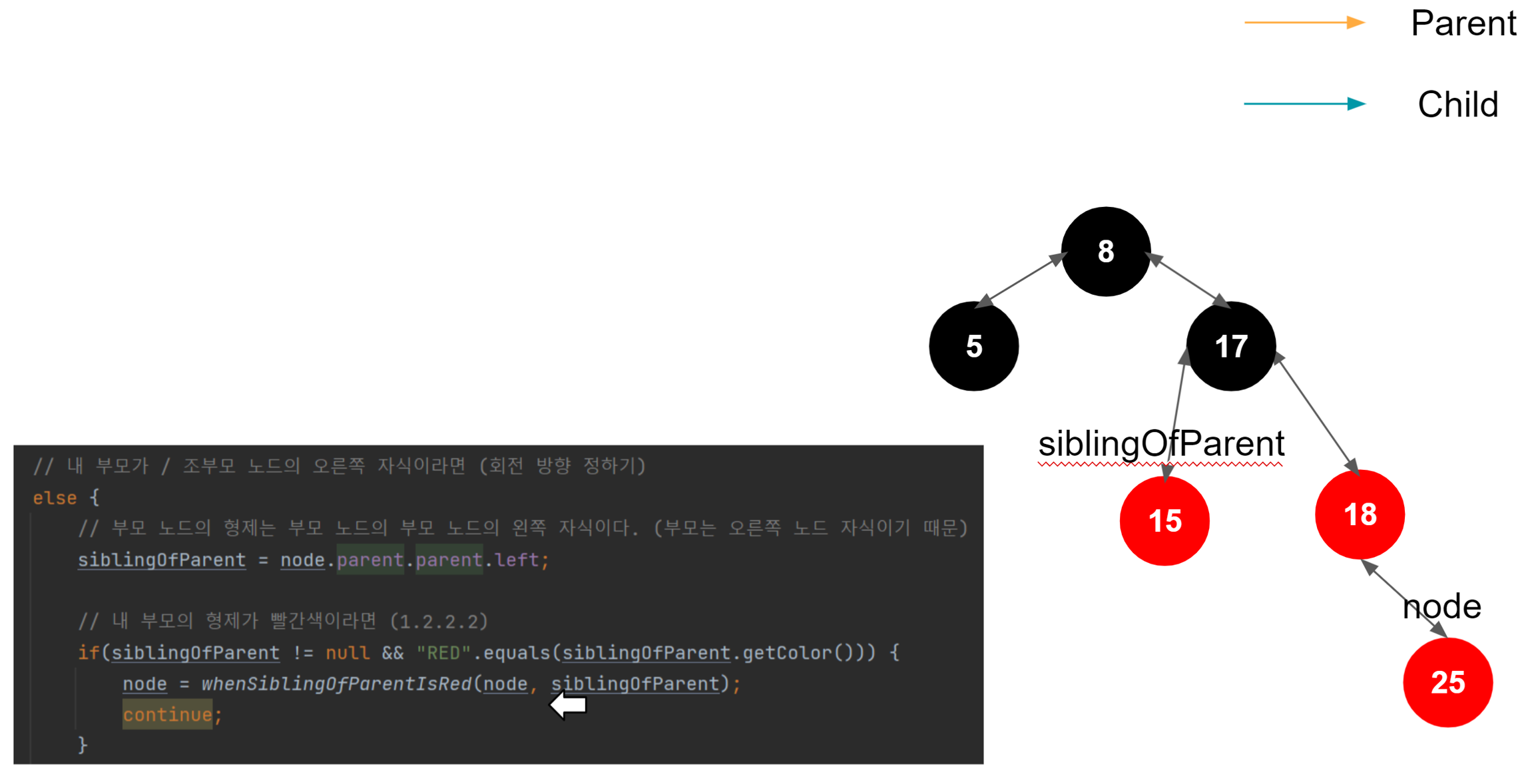
노드의 부모의 형제가 빨간색이라면 현재 노드의 부모와 부모의 형제의 height 차이는 없게 된다. 왜냐하면 레드 블랙 트리 특성상 루트 노드에서 리프 노드까지 가는 도중 만나는 검은색 노드의 숫자는 같아야 하기 때문이다.

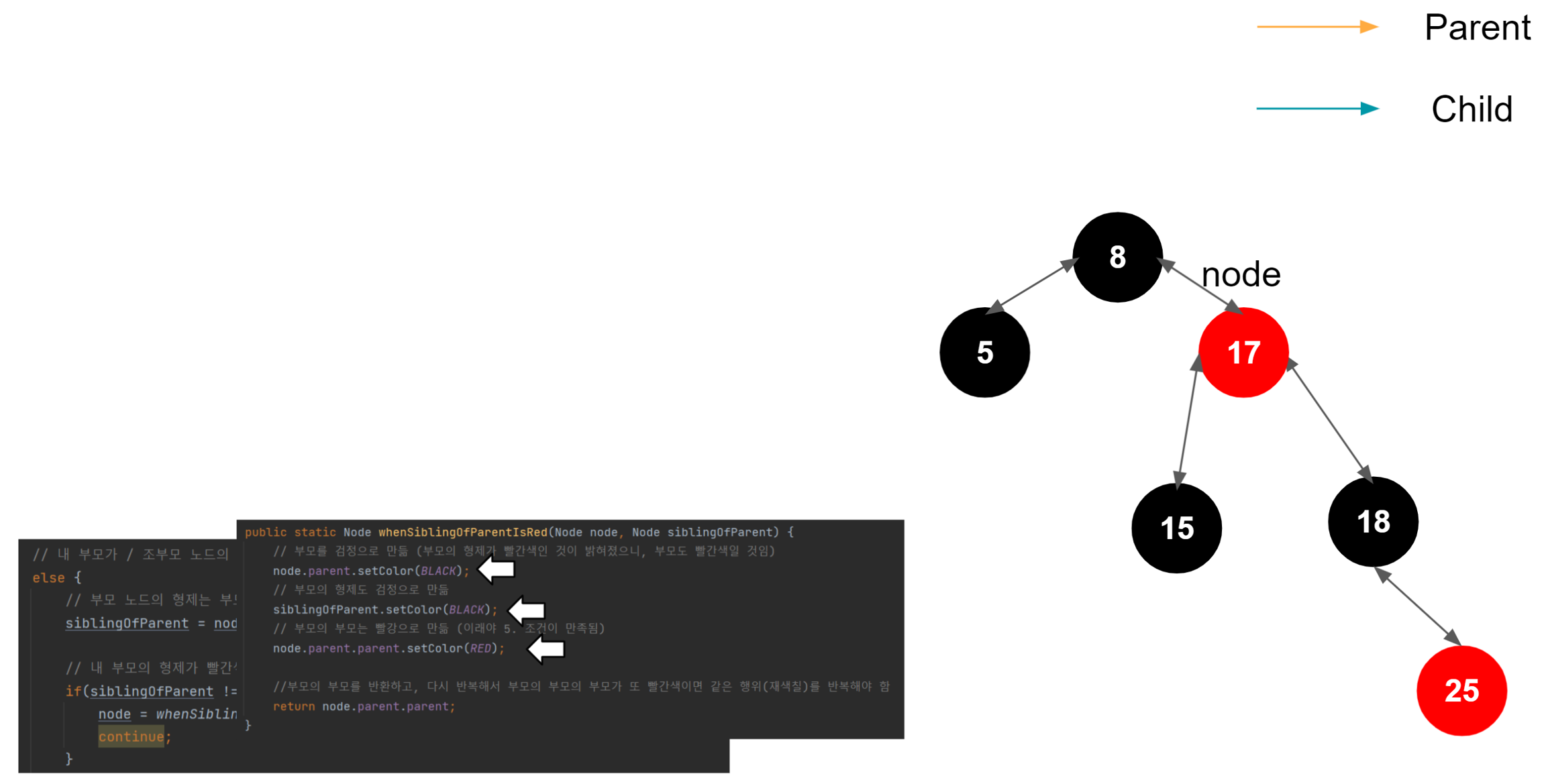
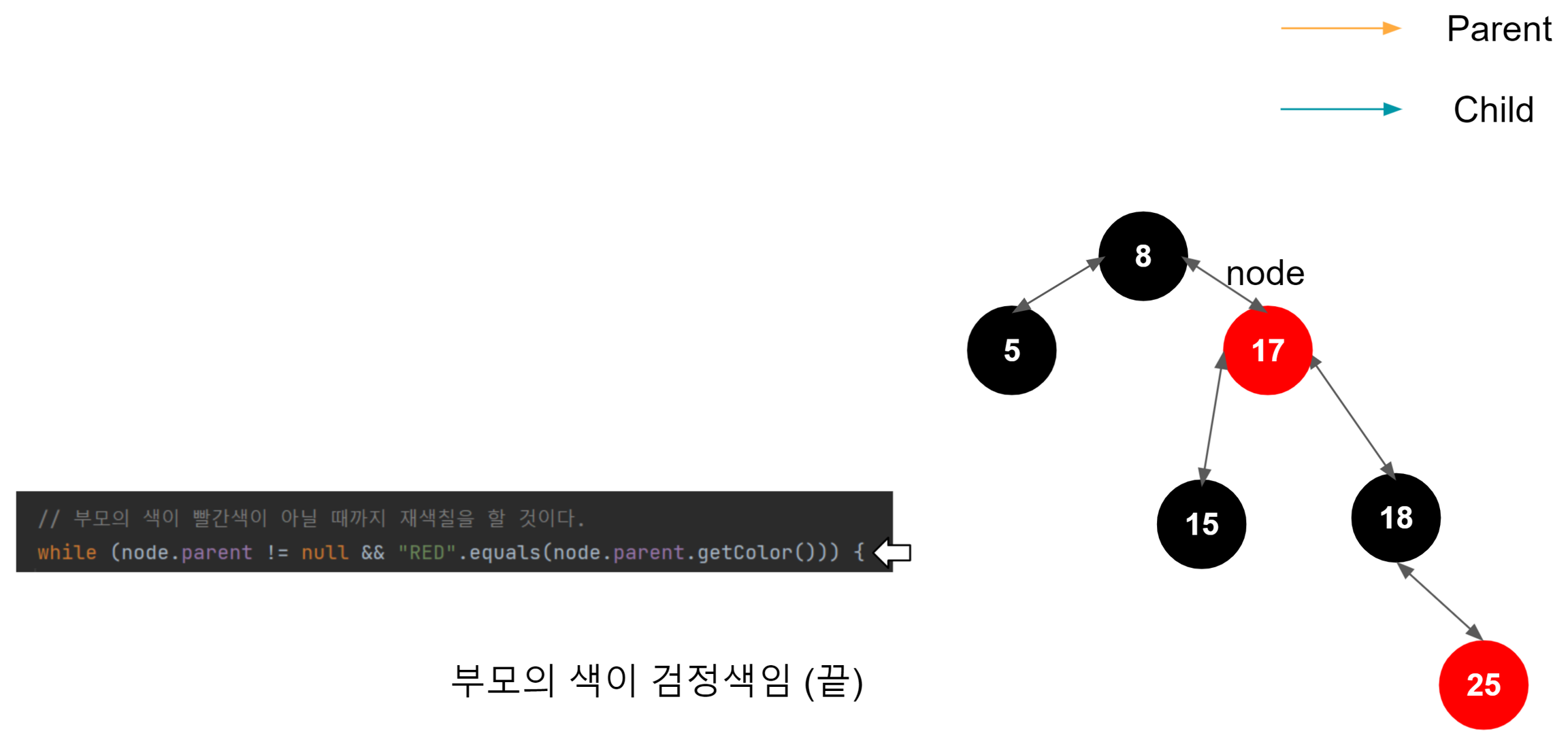
40 삽입

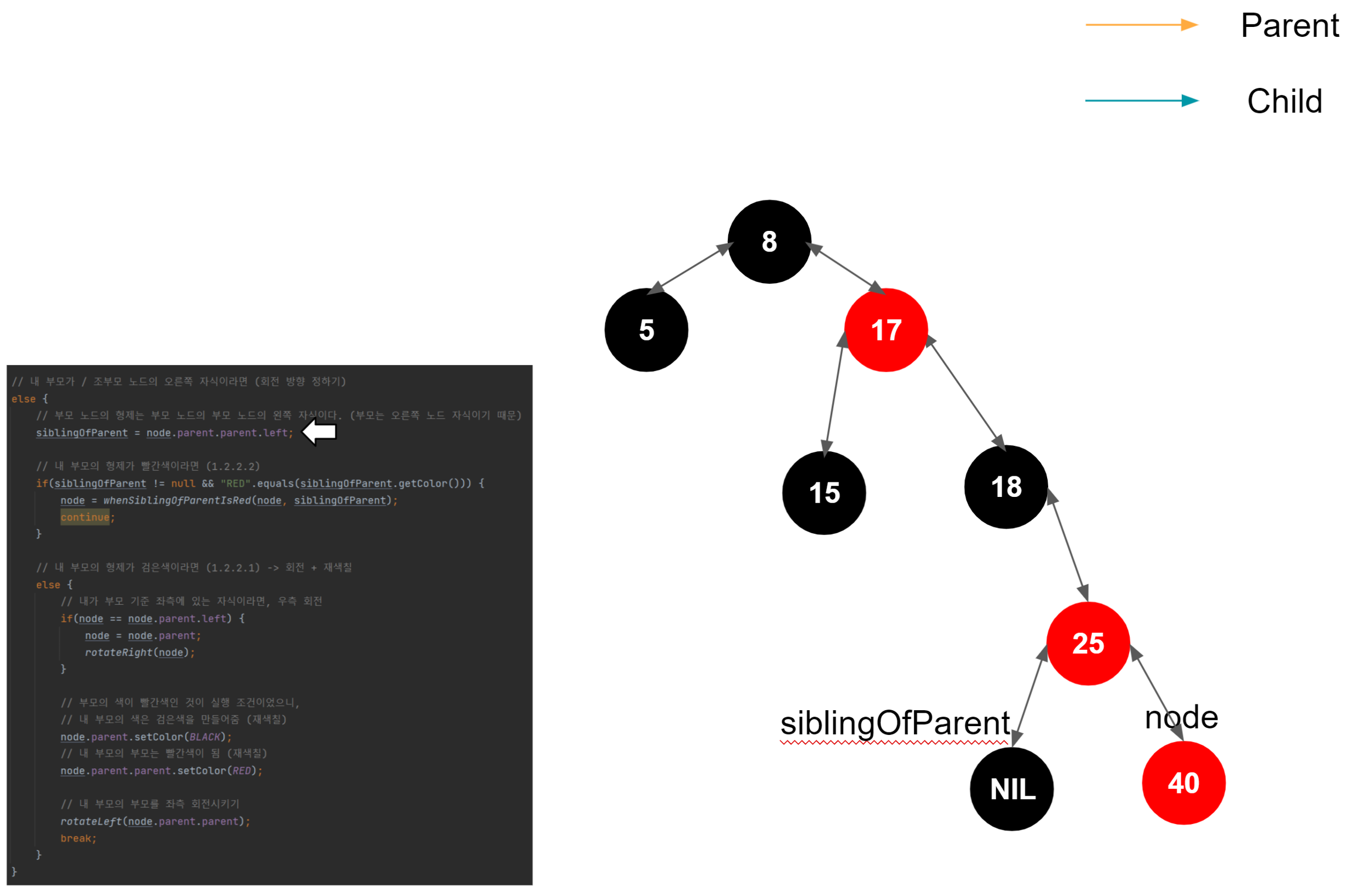
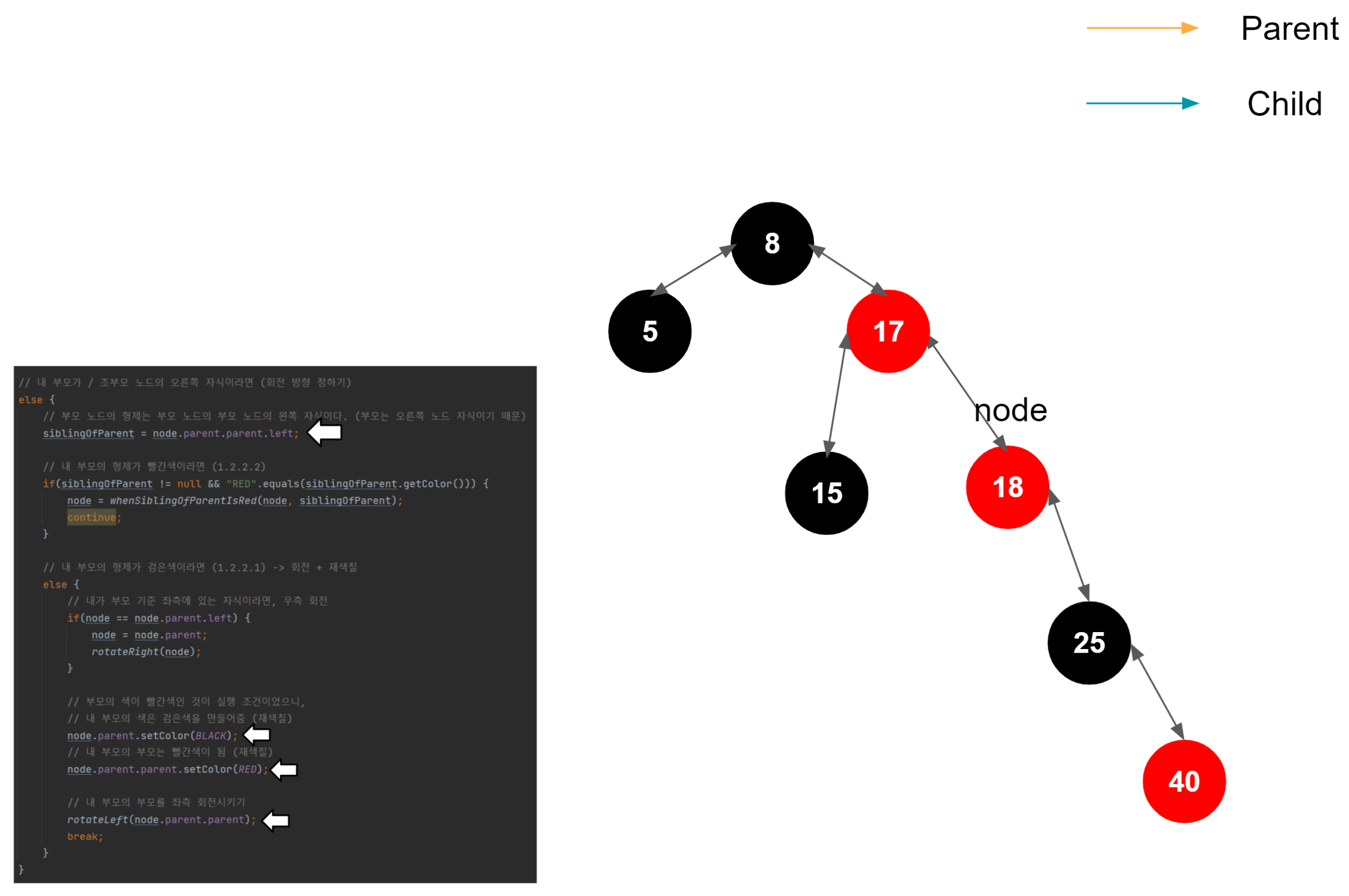
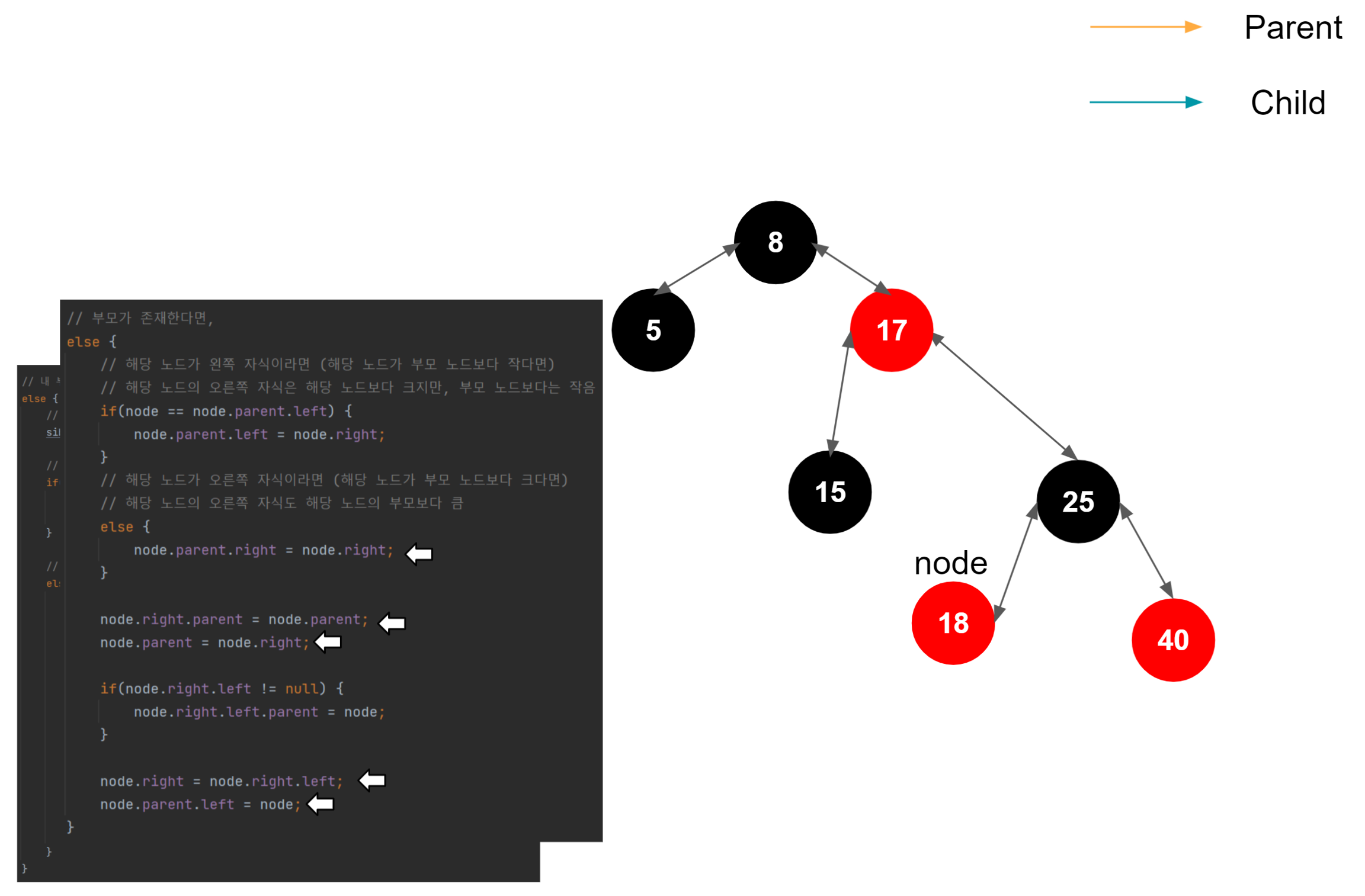
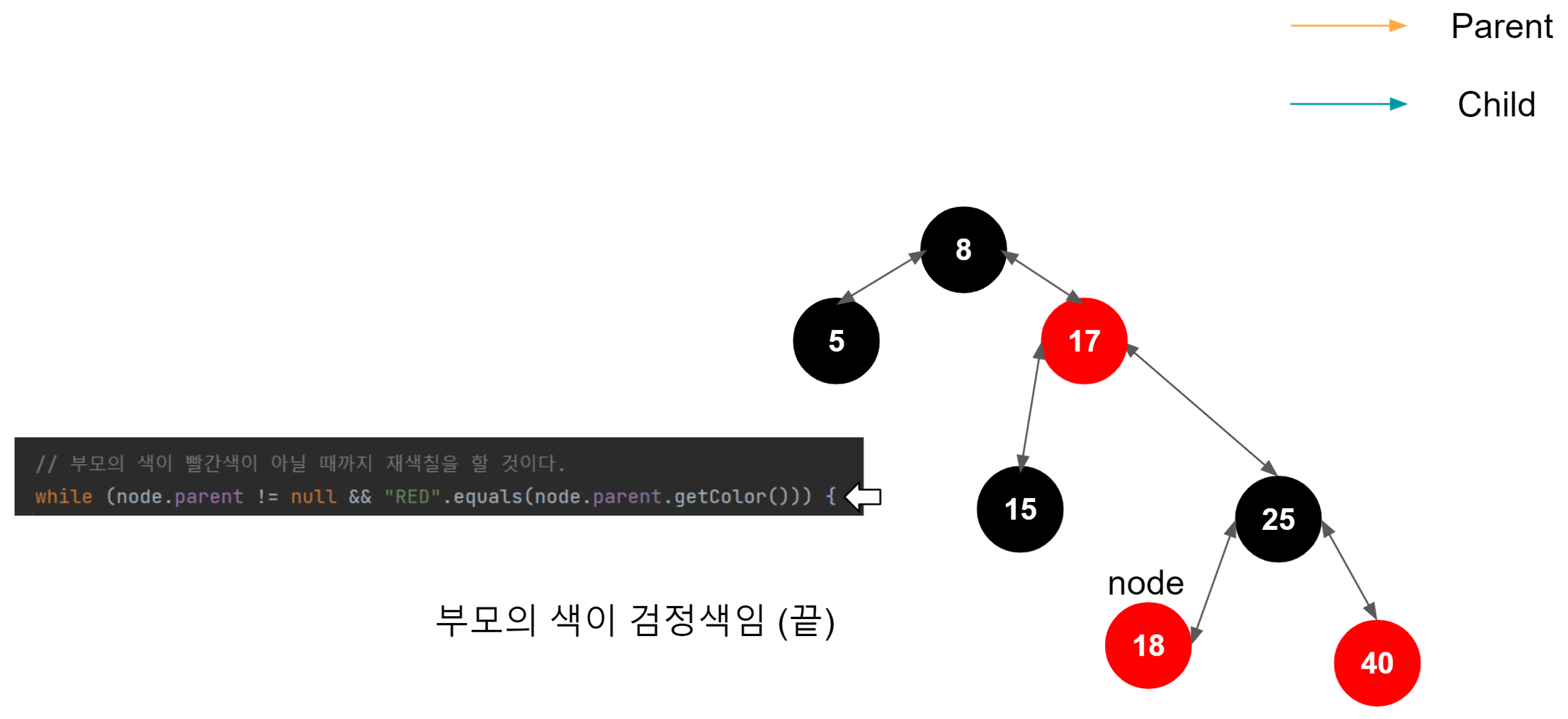
참고했던 링크들 https://junboom.tistory.com/18 https://zeddios.tistory.com/237 https://coding6467.tistory.com/11 https://www.cs.usfca.edu/~galles/visualization/RedBlack.html